Physicist Peter J. Lu stands beneath tile spandrels at the Darb-i Imam shrine in Isfahan, Iran.

The intricate tilework on that building inspired him to dig into the history of Islamic art, and eventually to prove that a number of medieval Islamic designs had at their heart patterns that modern mathematicians have only recently been able to describe. In fact, the young physics whiz found on Islamic buildings the very geometric forms identified by British mathematician Sir Roger Penrose as the foundation elements for elaborate, non-repeating patterns. Lu’s research shows that these patterns had been applied long before Penrose’s discovery—in fact, more than 500 years earlier.

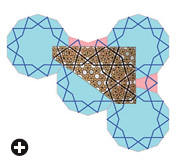
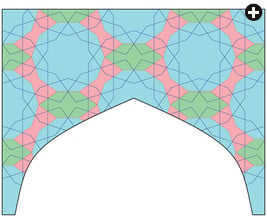
Each spandrel maps to a nearly perfect Penrose quasi-crystal pattern, which consists of strapwork—the heavy blue lines above left inscribed in large decagons (blue)—that overlies a pattern of smaller white decagons. To analyze it as a Penrose quasicrystal pattern, Lu divided it into Penrose’s “kites” and “darts” (fine black lines above right) and then superimposed curving red and blue ribbons that, as they intersect each side, demonstrate a non-periodic pattern: It looks regular, but it is not actually repetitive. As the pattern expands toward infinity, the ratio of kites to darts approaches the golden ratio, or phi—about 1.618.

Conventional patterns that completely cover a surface, such as those found in floor tilings, are repetitive: Any patch can be moved a certain distance to cover an exactly matching part elsewhere in the pattern. Some shapes, such as hexagons, can only be arranged in such periodic patterns. Many other shapes can be arranged periodically as well as non-periodically, that is, in a pattern that does not repeat itself no matter how far a patch is moved. For many years, mathematicians believed that there were no shapes that could only be arranged non-periodically. In the 1960’s, experts did discover sets of shapes that force non-periodic patterns, but they required elaborate rules and large numbers of different shapes—more than 20,000 in the template described in one published paper.

TOPKAPı SCROLL: COURTESY GÜLRU NECIPOğLU

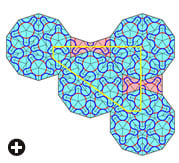
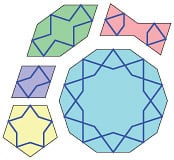
In the Topkapı Scroll, which lays out principles of Timurid design, this pattern of five- and ten-pointed stars, top, demonstrates that, by the 15th century, craftsmen were using girih tiles to create complex patterns. The five girih tiles are inscribed in blue, above right, in each of five equilateral polygons—a hexagon (green), a bowtie (pink), a decagon (blue), a rhombus (purple) and a pentagon (yellow). An example of each polygon is tinted in the Topkapı Scroll, above center; a fully tinted analysis, in which the girih tiles are outlined in blue and the polygons in red, appears above.

Penrose’s breakthrough, in 1974, was to identify a set of only two shapes—nicknamed “kites” and “darts”—that create an exclusively non-periodic tiling, which became known as the Penrose pattern. Despite their non-periodic nature, the resulting configurations are not chaotic. Rather, they fit together in a way that is predictable but difficult for the brain to perceive. As the pattern made of the two Penrose shapes expands, the proportion of kites to darts approaches the golden ratio, or phi (≈1.618). The golden ratio, a name first used by Leonardo da Vinci (Latin sectio aurea, “golden section”), is a balance found in nature, as well as in esthetically pleasing artificial constructs, that has attracted the attention of geometers ever since the time of ancient Egypt.

In 1984, a physicist for the first time observed a three-dimensional example of a Penrose pattern in the material world. A specific alloy produced in the laboratory showed the kind of symmetries and non-periodic patterns previously known only theoretically from Penrose’s kites and darts. This discovery was described as a “quasicrystal” because it shared some defining properties of crystals but lacked their regular repeating structure. Subsequently, many more synthetic, laboratory-made quasicrystals were produced, and the first known natural quasicrystal was described in 2009. Penrose patterns were also applied in a number of man-made products including puzzles and, predictably, tiles. One manufacturer even chose them for its quilted toilet paper—and was promptly sued by Penrose for copyright infringement.

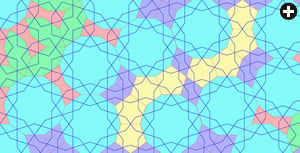
The tilework on the Bukhara madrasa is an example of the stylized geometric strap-work—typically based on star or polygon shapes—that is emblematic of traditional Islamic ornamentation. This form of design is known as girih patterns, from the Persian word for “knot.” It is generally believed that such designs were constructed by drafting zigzag outlines with only a straightedge and a compass. But Lu perceived something more: “I saw five-fold and ten-fold stars, which immediately aroused my curiosity about how these tilings had been made.” He wondered how Islamic craftsmen had been able to design such elaborately symmetrical patterns centuries before the advent of modern mathematics.

Lu returned to Harvard with this question in mind and set to mapping the abundant pentagonal and decagonal motifs of the Uzbeki madrasa. Sifting through hundreds of additional images of other medieval Islamic buildings, he was able to identify five underlying shapes that account for the geometric complexity of their designs: a decagon, a pentagon, a hexagon, a rhombus and a “bowtie.” Although these are not immediately visible, they form the basis for the most complex, or “knotty,” girih designs. Lu describes these five shapes as “girih tiles” and regards them as the tools that enabled craftsmen to construct highly

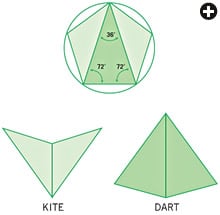The kites and darts that can be combined to make a non-periodic Penrose quasicrystal pattern originate when an isosceles triangle is inscribed within a pentagon (top). Notice that the result is not one triangle but three: the isosceles triangle (dark tint) and two identical obtuse triangles (light tint). The two obtuse triangles combine to make a kite; two of the isosceles triangles combine to make a dart.

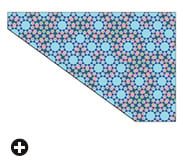
Of all the examples of Islamic tilework Lu examined, the most intriguing was on the portal of the Darb-i Imam shrine in Isfahan in central Iran, a building completed in 1453. Even amid the copious historical riches of Isfahan, the Darb-i Imam is renowned for the magnificence of its enameled tile decorations, and they prompted another breakthrough in Lu’s understanding of medieval Islamic geometry. While reading an article on Penrose patterns, he suddenly recognized their resemblance to the designs on the huge entryway to the shrine. “I discovered this in the evening on Christmas Eve,” he recalls. “I then stayed up all night to start mapping the tilings.” The similarity of their underlying shapes to Penrose’s kites and darts led Lu to see his girih tiles in a new light. He was astonished to find that the Darb-i Imam tilework formed a near-perfect Penrose pattern.

LEFT: H. SCHMID, DIE MADRASA DES KALIFEN AL-MUSTANSIR IN BAGHDAD (ZABERN)
Right: Girih pattern analysis of decagonal strapwork above an arch (left) in the Abbasid al-Mustansiriyya Madrasa in Baghdad, Iraq, which dates to between 1227 and 1234.

The girih tiles make possible large-scale patterns because each edge has the same length, allowing different combinations to be aligned. What is more, every edge is intersected at its midpoint by two decorating lines at fixed angles, which ensures that the lines continue across the edges from one tile onto another. A further innovation was achieved by dividing girih tiles into smaller ones to create overlaid patterns at two different scales, a method mathematicians call “self-similarity transformation.” This kind of subdivision, combined with the symmetry imposed by the shapes of the girih tiles, creates non-periodic tiling, just like the Penrose patterns.

W. B. DENNY / PETER J. LU
Girih pattern analysis of a decorated arch in the Sultan’s Loge of the Ottoman-era Green Mosque in Bursa, Turkey, which was completed in 1424.

Lu contacted his undergraduate adviser—Paul J. Steinhardt of Princeton University, a pioneer in the study of quasi-crystals—and they teamed up to write an article about this discovery, published in the journal Science in 2007. They argue that the introduction of girih tiles around the year 1200 marked “an important breakthrough in Islamic mathematics and design” that allowed for an entirely new way of conceptualizing and designing patterns. This paved the way for the further development of the subdivision that made possible the non-periodic pattern on the Darb-i Imam shrine. Their article received wide coverage in academic journals, as well as in newspapers as diverse as The New York Times and Iran Daily. Their findings were all the more remarkable for showing that the five girih tiles could be further reduced to just two shapes: the very same kites and darts described by Penrose.

This discovery raised two further questions: How much of the mathematics underlying the girih tiles was understood by the Islamic craftsmen who designed and used them more than 500 years ago? And was the use of Penrose patterns coincidence or the deliberate application of highly advanced mathematical knowledge?

Such is the nature of an institution like Harvard that an expert is never far away: Lu approached Gülru Necipoğlu, a professor of Islamic art and architecture with a special interest in tiles. She referred him to her 1995 book The Topkapı Scroll: Geometry and Ornament in Islamic Architecture. The scroll takes its name from the Topkapı Palace in Istanbul, the administrative center of the Ottoman Empire, where it was found. Believed to date from the late 15th or early 16th century, the scroll shows a succession of two- and three-dimensional geometric patterns over its 29.5-meter (almost 97') length. The patterns are not accompanied by text, but use grid systems and color-coding to highlight symmetries and distinguish three-dimensional projections, suggesting that the scroll was a repository of designs for master craftsmen rather than a showcase for potential patrons.

Crucially, the Topkapı Scroll does not represent the architectural style of the Ottomans, but rather the Timurid design traditions of Iran and Central Asia. The Timurid dynasty was of Mongol origin and ruled over a large empire encompassing much of Central Asia, Persia and Mesopotamia from the mid-14th century until 1506. Timurid architecture and design drew heavily on earlier Persian models, which developed into a distinct style particularly noted for its emphasis on geometry and symmetry.

DAVID JAMES: QUR’ANS OF THE MAMLUKS (THAMES & HUDSON)
A decagon, surrounded by bowties and hexagons, forms the basis of this cover of a Mamluk copy of the Qur’an that dates to the early 14th century.

Because Isfahan’s Darb-i Imam is an example of Timurid architecture, it can be linked to the designs in the Topkapı Scroll and thus offers direct insights into the level of understanding craftsmen had of the complex patterns they produced for the shrine. In fact, in the scroll’s complex multicolored designs, Lu observed an underlying pattern drawn in faint red ink: He recognized the five girih tiles and now had direct historical documentation for their use. This proved that the pattern on the shrine was not a fluke but rather part of the design repertoire of master craftsmen in that region and period. It also confirmed Necipoğlu’s view that the Topkapı Scroll had been used intensively by architects and artisans in the construction of buildings such as the Darb-i Imam.

Indeed, drawings such as those in the Topkapı Scroll could have served as pattern-books for the artisans who fabricated the tiles, and the shapes of the girih tiles then dictated how they could be combined into large patterns. In this manner, the craftsmen who actually did the tilework could construct highly complex designs without resorting to mathematics and without necessarily understanding their underlying principles. Nonetheless, while the efficiency of this method is illustrated by the high quality of the pattern at the Darb-i Imam shrine—when it is mapped to Penrose tiles, there are only 11 defects among 3700 tiles—it is the most mathematically complex pattern yet discovered, and Lu finds it “quite reasonable to believe that its particular designers knew what they were doing mathematically.”

The achievement of the Darb-i Imam tiling shows that “Islamic designers had all the elements needed to construct perfect quasicrystalline patterns,” according to the researchers. However, they also believe that these designers had only an incomplete understanding of these elements, highlighting the different priorities of the modern discipline of theoretical mathematics and the practical application of geometric processes by the master craftsmen of the past.

In her study of the Topkapı Scroll, Necipoğlu notes the parallel between the girih style and the contemporary Gothic style practiced by European artisans. Designers of both styles were concerned with using their inventories of geometric shapes to create “a maximum diversity of forms,” she writes, a skill quite different from that of the mathematician. Much remains to be learned about the Muslim designers and craftsmen, none of whom has been identified by name in the historical records. Although they are anonymous, Lu and Steinhardt pay them tribute by concluding that their “geometrical sophistication led the medieval world.”

ABOVE, Right: NEIL BANAS
Left: In Bukhara, Uzbekistan, this decagonal pattern, ornaments the portal of the khanqah (lodging complex) of Nadir Divan Beg, built in the early 17th century and restored in the 1990’s. Right: In the early 15th century, Timurid craftsmen in Samarkand produced this bas-relief pattern on the Ulugh Beg Madrasa.

The notion that the knowledge of Penrose patterns was anticipated—although never fully elaborated—in 15th-century Persia and elsewhere in the Middle East and Central Asia is not as unexpected as it might first seem. While many of the terms and concepts used in modern mathematics hark back to the Greek classical period, much of this ancient knowledge was lost to the Christian world for many centuries. Although the view of a European “dark age” has been rightly rejected by historians, it is true that a great deal of classical scientific knowledge had dropped out of circulation in medieval Europe. Islamic societies, on the other hand, were able to actively seek out, preserve and build on this knowledge. By this means, many of the scientific breakthroughs of Renaissance Europe were inspired and informed by the intellectual achievements of Islamic societies.

Take Euclid, the famed “father of geometry,” whose theorems are still studied by schoolchildren. The translation of his text Elements into Arabic was sponsored by the Abbasid caliph Harun al-Rashid in the late eighth century. Subsequent caliphs continued to encourage learning by supporting the translation of the writings of Archimedes, Apollonius, Ptolemy and others. These translations were not prestige projects done for their own sake, but were made by mathematicians and scientists to facilitate their ongoing research. Access to this corpus of ancient knowledge allowed them to significantly improve upon it.

Wrapping a column in the early–19th-century Tash Hauli palace in Khiva, Uzbekistan, a strapwork pattern of decagons and pentagons is filled with vegetal arabesques that maintain five-fold and ten-fold symmetry.

Around 830, the Persian mathematician Muhammad ibn Musa al-Khwarizmi made a mathematical breakthrough: He incorporated Euclid’s geometry into a unifying theory that became known as algebra (from the Arabic jabara). This spawned a wave of new mathematical ideas expounded by al-Khwarizmi’s successors over the next centuries. The flowering of scientific brilliance from the ninth to about the 13th century—a period often described as the “golden age” of Islamic science—was promoted by the patronage of Muslim rulers and the intellectually stimulating atmosphere in their capitals. Scholars from all over the Islamic world gathered in cities such as Baghdad, Cairo and Córdoba to exchange ideas, peruse the great libraries and make names for themselves.

Not all of them were Muslims—many Jews, Christians and Zoroastrians made important contributions—nor did they all write in Arabic: Persian in particular remained an important lingua franca for scholars from different backgrounds. Neither did these scholars limit their research to the works of the ancient Greeks. As the Islamic world expanded, it drew in scientific knowledge from the civilizations with which it came into contact, especially India and China. For example, mathematics benefited immensely from the adoption of the ancient Indian positional number system, in which the lowest-value digit is on the right (as in “25,” where the five represents how many ones are in the number and the two represents how many 10’s) and which includes the concept of “zero,” the empty position. Muslim mathematicians adopted Indian numerals around the early ninth century: A few years before his famous book on algebra, al-Khwarizmi wrote a work entitled On Calculation with Hindu Numerals. The introduction of the Hindu–Arabic numeral system to Europe in the early 13th century is credited to Leonardo of Pisa (known as Fibonacci), who is thought to have learned about it from Muslims in North Africa. Like that system, many other mathematical concepts preserved or developed by Muslim mathematicians found their way north, providing the foundations for a reinvigoration of the sciences in Europe.

It’s interesting that the famous number sequence named after Fibonacci—1, 1, 2, 3, 5, 8, 13, 21 and so on, where each term is the sum of the two previous terms—is closely related to the golden ratio, 1.618…, that is visible in the Penrose patterns. Specifically, the ratio of successive Fibonacci numbers converges on that number: 1/1 = 1, 2/1 = 2, 3/2 = 1.5, 5/3 = 1.666, 8/5 = 1.6, 13/8 = 1.625, 21/13 = 1.615 and so on.

On this panel in the Shah Mosque in Isfahan, Iran, ten-pointed stars—none of them shown completely —anchor the edges of a pattern in which four of the five girih shapes can be found. Both the stars and the scallop-edged hexagons are placed according to an underlying design of still more decagons and pentagons. The stars’ incompleteness reminds the viewer that the pattern actually extends into infinity.

For all their tantalizing glimpses into medieval scientific knowledge, the designs of the Darb-i Imam and other Islamic buildings must also be understood in their religious context. Geometric patterns in Islamic architecture and ornamentation were used as much for spiritual as for artistic reasons. As Robert Irwin writes in his study of Islamic art, such patterns may have been viewed “as exteriorized representations of abstract, even mystical, thought”—aiming to inspire contemplation or to make a statement about the imponderable harmonies of a divinely ordered universe. Sufism in particular is closely linked to the practice of geometry, above all in the form of symmetries, as a way of giving physical expression to mystical thought.

The girih designs are thus comparable to Gothic art and architecture in another sense, namely in their shared ambition to embody spiritual cogitation and emotion through geometry. The real significance of the magnificent tiling of the Darb-i Imam lies not in any kind of cultural one-upmanship about who first conceived a certain idea or technique, but rather in the remarkable trajectories of ideas and scientific endeavors through time.

These new discoveries thus remind us not only of the momentous achievements of Islamic societies in the past, but also of the history and value of cross-cultural interac-tion and exchange. Perhaps unsurprisingly, Peter Lu himself advocates taking a scien-tific approach to tracing this interaction. “Mathematics is the only universal language, and has shown itself consistently capable of connecting people through time and space,” he says. His remarkable findings are a reminder not only of the historical interconnections between societies and cultures, but also of the promise held by further collaborations between scholars specializing in the sciences and the arts.

Sebastian R. Prange (s.prange@ubc.ca) holds a doctorate in history from the School of Oriental and African Studies at the University of London. Currently a postdoctoral fellow at the University of British Columbia, he researches the organization of Muslim trade networks in the pre-modern Indian Ocean, with a special focus on southern India.